在实证研究中,因果识别始终是核心难题。如何精准捕捉个体行为对政策的响应、量化制度设计对市场的影响,是学者们长期探索的关键方向。近年来,一种名为“群聚分析法”的前沿实证方法异军突起,凭借其对非连续制度场景的独特适配性,成为连接结构式估计与简约式估计的重要桥梁,在税收、社会保障、企业决策等多个经管领域展现出强大的解释力,相关研究成果频频登上国际顶刊(张航和范子英,2019)。今天,我们就系统拆解这一科研利器,从原理内核、优劣辨析到具体应用,带大家全面掌握其核心逻辑与使用场景。
一、群聚分析法的核心原理
群聚分析法的核心逻辑源于对个体理性决策的观察:当制度设计中存在明确的阈值,如税收起征点、政策资格线、监管标准等,个体为追求自身利益最大化,会主动调整行为以趋近或规避该阈值,从而在数据分布上形成明显的“聚集效应”。该方法通过捕捉这一独特的数据特征,构建反事实框架,进而量化行为弹性、政策效应等关键经济参数。
(一)核心前提:非连续制度与理性决策假设
群聚分析法的应用需满足两个基础前提:一是存在非连续型制度场景,二是个体具备有限理性决策能力(冯晨等,2023)。
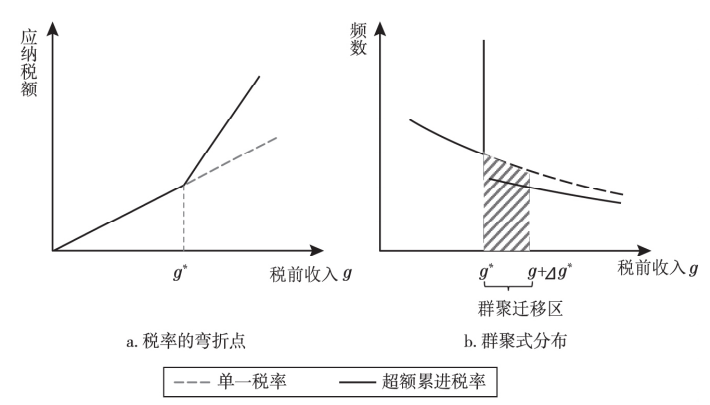
从制度场景来看,核心是存在明确的“制度弯折点”或“制度断层点”。其中,弯折点指政策待遇随变量变化呈现斜率突变,如累进税制中,当收入超过某一阈值后,边际税率突然提高,此时收入分布在阈值下方可能出现聚集;断层点则指政策待遇出现水平跳跃,如达到特定经营规模的企业需额外承担环保监管成本,可能导致企业规模在阈值下方形成聚集。这类非连续制度广泛存在于经管领域,为群聚分析法提供了天然的研究场景。
从个体决策来看,该方法假设个体具备有限理性,能够感知制度阈值的存在,并愿意付出一定成本调整行为以获取收益(或规避损失)。例如,纳税人会通过调整申报收入避开更高税率区间,企业会通过优化产能规模规避严格监管,这类主动调整行为正是形成聚集效应的核心动力。若个体对制度阈值无感知,或调整成本过高无法实施,则难以形成可观测的聚集特征,方法适用性会大幅下降。
(二)识别逻辑:聚集效应与反事实框架的构建
群聚分析法的识别核心的是对比差异:通过对比阈值附近的实际数据分布与无政策干预下的反事实分布,分离出制度因素对个体行为的净效应。其核心逻辑可概括为“观察聚集—构建反事实—量化效应”三步闭环。
首先,观察并验证聚集效应的存在。在无政策干预的理想状态下,个体行为变量(如收入、企业规模、移民数量等)应呈现平滑的连续分布;而当存在非连续制度时,理性个体的调整行为会打破这种平滑性,在阈值附近形成“峰值”(聚集区)和“谷值”(规避区)。例如,在税收政策中,若某一收入水平对应边际税率的跃升,纳税人会尽量将收入控制在该水平以下,导致收入分布在阈值下方出现明显峰值,上方则因部分个体的规避行为出现谷值,这种“峰谷并存”的特征就是聚集效应的直接体现。
其次,构建反事实分布。这是群聚分析法的关键步骤,核心是模拟“若不存在该非连续制度,个体行为变量的分布状态”。由于现实中无法直接观测无政策场景,研究者需通过合理的统计方法进行推断,常用策略包括:一是利用阈值远离区域的平滑数据进行插值或拟合,如采用多项式回归对阈值两侧非聚集区域的数据进行拟合,得到平滑的基准分布;二是引入安慰剂检验,通过虚构阈值(如将真实阈值平移一定范围)或选取不受政策影响的对照组,验证拟合的反事实分布的可靠性;三是控制其他混淆因素,如个体特征、时间趋势、区域差异等,确保反事实分布仅反映“无政策干预”的自然状态。
最后,量化因果效应。通过对比实际分布与反事实分布的差异,可精准测度个体行为对制度的响应程度。核心量化指标包括行为弹性(如税收弹性、移民弹性)、政策规避程度、最优化摩擦等。例如,通过计算聚集区的“超额个体数量”(实际分布与反事实分布在峰值区域的差值),可量化有多少个体为规避不利政策调整了行为;结合成本收益分析,还可进一步估计个体的行为弹性——即政策待遇变化对个体行为的影响程度,这一参数是评估政策有效性的核心依据。
二、群聚分析法的优劣辨析
作为一种新兴的因果识别工具,群聚分析法在科研中展现出独特优势,但其应用也受场景、数据等多重因素限制。全面辨析其优劣,是合理运用该方法的前提。
(一)核心优势
(1)对非连续制度场景的精准适配,填补传统方法空白(崔小勇等,2025)。在经管领域,双重差分法(DID)、断点回归法(RDD)是常用的因果识别方法,但两者均有明确的适用边界:DID依赖政策的外生性冲击与对照组的合理选择,RDD则要求个体无法精确操控阈值变量。而群聚分析法专门针对“个体可主动调整行为的非连续制度场景”设计,当存在税收阈值、资格线等可感知的制度边界时,其识别效果优于传统方法。例如,在研究纳税人对累进税制的响应时,个体可主动调整收入以规避高税率,此时RDD的“不可操控性”假设不成立,而群聚分析法则可通过捕捉收入分布的聚集特征,精准识别税收政策的效应。
(2)兼具理论严谨性与实证灵活性,连接结构与简约估计。在实证研究中,结构式估计需明确设定理论模型(如效用最大化模型),虽能揭示因果机制,但模型假设较强;简约式估计(如DID、RDD)无需严格理论假设,可直接测量政策效应,但难以深入解释行为背后的机制。群聚分析法则实现了两者的桥梁作用:在结构估计中,可通过聚集特征验证理论模型的预测(如效用最大化假设下的行为调整方向),并估计模型中的关键参数(如风险偏好、调整成本);在简约式估计中,可无需严格理论假设,直接通过分布差异测量政策效应,兼顾了理论深度与实证灵活性。
(3)数据需求相对灵活,适用范围广泛。群聚分析法的核心数据需求是“包含制度阈值的微观行为数据”,这类数据在经管领域较为丰富,如税务部门的个体税收数据、统计部门的企业普查数据、社保部门的保障资格数据等。与需要面板数据的DID相比,群聚分析法可基于截面数据实现识别,降低了数据收集难度;同时,其应用场景覆盖税收、社保、移民、企业决策、交通管制等多个领域,具有极强的通用性。
(4)结果直观易懂,政策启示明确。群聚分析法通过分布形态的可视化(如核密度图)直接呈现个体行为对政策的响应,结果直观易解读;其估计的行为弹性、规避程度等参数,可直接为政策优化提供量化依据。例如,若研究发现某税收阈值附近聚集效应显著,说明纳税人规避行为强烈,政策设计可能存在不合理之处,需通过调整税率结构、降低调整成本等方式优化政策;若聚集效应微弱,则可能意味着政策对个体行为影响较小,或个体调整成本过高,需重新评估政策的有效性。
(二)主要局限性
(1)场景适用性受限,依赖非连续制度的存在。群聚分析法的核心前提是“存在可感知的制度阈值”,若研究问题对应的制度是连续的(如线性税率、渐进式监管),或阈值不明确(如模糊的政策指导意见),则无法形成可观测的聚集效应,方法无法适用。这一局限性导致其无法用于分析无明确阈值的政策或市场现象,如普遍性的补贴政策、完全竞争市场中的价格形成机制等。
(2)反事实分布构建存在主观性,影响结果可靠性。反事实分布的拟合依赖于研究者对模型的设定,如多项式回归的阶数、带宽的选择、混淆因素的控制等,不同设定可能导致结果存在差异,存在一定的主观判断空间。例如,若选择过高的多项式阶数,可能导致拟合曲线过度拟合数据噪声;若带宽选择过小,则样本量不足,影响拟合精度。尽管可通过稳健性检验缓解这一问题,但无法完全消除主观设定的影响。
(3)对数据质量要求较高,易受测量误差影响。聚集效应的识别依赖于变量分布的精准测量,若数据存在测量误差(如个体收入申报不实、企业规模统计偏差),可能掩盖真实的聚集特征,或导致虚假的聚集效应。例如,若纳税人因统计口径问题误报收入,可能导致收入分布在阈值附近出现虚假峰值,干扰对政策效应的判断。此外,样本量不足或数据覆盖范围过窄,也会影响反事实分布的拟合效果,降低结果的可信度。
(4)难以完全规避“多重阈值”与“一般均衡效应”的干扰。在现实场景中,可能存在多个相互关联的制度阈值(如不同税种的起征点、不同层级的监管标准),个体行为可能同时受多个阈值影响,导致聚集效应相互叠加,难以分离单一政策的影响;同时,个体的调整行为可能引发一般均衡效应(如大量企业规避监管导致市场竞争格局变化),而群聚分析法通常聚焦于个体层面的局部效应,难以捕捉这类宏观层面的间接影响,可能导致对政策效应的低估或高估。
三、总结与展望
群聚分析法以其对非连续制度场景的精准适配性、连接结构与简约估计的独特优势,成为科研中极具价值的因果识别工具。其核心逻辑是通过捕捉个体在制度阈值附近的聚集效应,构建反事实框架,量化行为弹性与政策效应,为政策优化提供量化依据(王贞等,2023)。尽管存在场景依赖、反事实构建主观性等局限性,但通过严谨的方法设计,如充分的稳健性检验、合理的模型设定,以及高质量的数据支撑,可有效缓解这些问题。
从应用前景来看,随着我国制度设计的精细化与微观数据的可获得性提升,群聚分析法的应用空间将进一步拓展:在政策评估层面,可用于更多细分领域的政策效应量化;在方法创新层面,可结合机器学习、空间计量等方法,优化反事实分布的构建精度,缓解多重阈值、一般均衡效应的干扰;在实践价值层面,其量化结果可直接为政策制定提供精准依据,助力实现“精准施策”的治理目标。
文献引用
[1] 崔小勇,卢鹏举,卢国军.规模依赖型减税政策与企业税收规避行为[J].管理世界,2025,41(11):104-141.
[2] 冯晨,刘冰,叶永卫.减税激励与异质性投资反应:来自小微企业的证据[J].管理世界,2023,39(11):38-62.
[3] 王贞,封进,刘一恒.门诊待遇非线性定价与住院率——来自城乡居民基本医保的证据[J].经济研究,2023,58(12):132-149.
[4] 张航,范子英.群聚分析法:原理、争议及应用前景[J].数量经济技术经济研究,2019,36(09):152-168.

