在因果推断领域，双重差分法（DID）与合成控制法（SCM）早已成为政策评估、效应识别的核心工具。但传统方法的固有局限，如DID对平行趋势假设的严格依赖、SCM对少量处理单元的适配性限制，始终是科研人员面临的痛点。2021年，诺贝尔经济学奖得主Imbens团队在《American Economic Review》发表重磅论文，提出一种融合两者优势的全新因果推断方法，合成双重差分法（Synthetic Difference-in-Differences，简称SDID）。该方法通过引入个体权重与时间权重，在保留传统方法核心逻辑的基础上实现了推断效率与稳健性的双重提升，迅速成为经管科研的前沿热点。

一、方法起源：传统方法的局限与SDID的突破

在SDID提出之前，DID与SCM是面板数据因果推断的两大主流方法，但两者均存在明显局限：

双重差分法（DID）的核心假设是“平行趋势假设”，即处理组与控制组在政策干预前的结果变量趋势保持平行。该方法适用于大量个体接受处理的场景，通过引入个体固定效应与时间固定效应控制非观测异质性，但当平行趋势假设不满足时（如处理组与控制组事前趋势存在系统性差异），估计结果会出现严重偏差。例如在评估某区域产业政策效果时，若处理组地区原本的经济增长趋势就显著高于控制组，直接使用DID会高估政策效应。

合成控制法（SCM）则通过对控制组个体赋予最优权重构建“合成处理组”，匹配处理组在干预前的多维特征与趋势，有效削弱了对平行趋势假设的依赖，适用于单个或少量处理单元的场景。但SCM存在两大缺陷：一是要求处理单元的特征必须位于控制单元特征的“凸包”内（即处理单元可由控制单元线性组合表示），否则权重估计会失真；二是难以进行有效的大面板推断，无法可靠估计处理效应的标准误与显著性。

SDID的提出正是为了突破上述局限。Arkhangelsky等（2021）通过构建包含个体权重与时间权重的加权双重差分框架，实现了三大突破：一是兼容大量处理单元与少量处理单元的场景；二是大幅放松平行趋势假设，无需处理组与控制组事前趋势完全平行；三是允许有效的大面板推断，估计量具有一致性与渐近正态性，可通过bootstrap、jackknife等方法可靠估计标准误。

二、核心原理：双重权重的构建与处理效应估计

SDID的核心逻辑可概括为双重加权与差分推断，具体分为三个步骤：

第一步：界定核心变量与研究框架。设定面板数据包含N个个体（其中N_tr个处理单元，N_co=N-N_tr个控制单元）、T个时期（其中T₀个处理前时期，T₁=T-T₀个处理后时期）。核心变量包括：结果变量Y_it（个体i在时期t的观测结果）、处理变量D_it（个体i在时期t是否接受处理，接受为1，否则为0）、个体固定效应α_i（控制个体层面不随时间变化的异质性）、时间固定效应γ_t（控制宏观层面随时间变化的共同冲击）。

第二步：估计双重最优权重。这是SDID与传统方法的核心差异所在，包括个体权重ω_i与时间权重λ_t的估计：

个体权重ω_i：仅应用于控制组个体，目的是匹配处理组与控制组的事前趋势。通过求解最优化问题，使控制组个体的加权平均结果与处理组的算术平均结果在处理前各时期尽可能接近（允许相差一个常数截距项，即无需水平一致，只需趋势平行）。为避免权重过度集中，通常会添加正则化惩罚项限制权重取值范围。例如在评估某政策对省份经济增长的影响时，个体权重会赋予那些与处理省份事前GDP增长趋势、产业结构、人口规模更相似的控制省份更高的权重。

时间权重λ_t：仅应用于处理前时期，目的是平衡处理前与处理后时期的权重分布，减少潜在的时间维度选择偏差。通过求解最优化问题，使控制组个体在处理前时期的加权平均结果与处理后时期的算术平均结果相差一个常数，确保时间维度的可比性。实践中同样会添加正则化惩罚项保证权重的唯一性。

第三步：计算处理效应。在获得最优个体权重与时间权重后，SDID通过加权双重差分公式估计平均处理效应（ATT）：ATT = E[Y_it(1) - Y_it(0)|D_it=1]，其中Y_it(1)为处理组的实际观测结果，Y_it(0)为通过加权控制组构建的合成反事实结果（即处理组未接受处理时的潜在结果）。具体公式可表示为：ATT=Σ(ω_iΣλ_tY_it(处理后)) - Σ(ω_iΣλ_tY_it(处理前))，通过加权后的前后差异与组间差异双重对比，精准识别处理效应。

三、模型设定：与传统方法的计量框架对比

从计量模型设定来看，SDID可视为双向固定效应（TWFE）模型的加权扩展形式。传统DID的TWFE模型为：Y_it=α_i+γ_t+βD_it+ε_it，其中β为处理效应，采用普通最小二乘（OLS）估计，不引入任何权重（即个体权重与时间权重均为1）。

SCM的模型则仅包含时间固定效应，通过个体权重加权估计：Y_it=γ_t+βD_it+Σ(ω_iY_it(控制组))+ε_it，不引入个体固定效应与时间权重。而SDID的加权TWFE模型为：Y_it=Σ(ω_iα_i)+Σ(λ_tγ_t)+βD_it+ε_it，通过个体权重ω_i与时间权重λ_t对固定效应进行加权，采用加权最小二乘（WLS）估计处理效应β。这种设定使其兼具DID的固定效应控制能力与SCM的权重匹配优势，成为更具一般性的计量框架。

四、合成双重差分的核心优势

（1）大幅放松平行趋势假设，提升推断可靠性。这是SDID最突出的优势。传统DID要求处理组与控制组事前趋势完全平行，而SDID通过个体权重匹配事前趋势，仅要求加权后的合成控制组与处理组满足“弱平行趋势”（即趋势差异为常数），大幅降低了方法适用的假设门槛。中国疾控中心的研究表明，在评估慢性病防控示范区建设效果时，由于部分地区事前健康行为趋势存在差异，传统DID估计出现偏差，而SDID通过权重匹配自动满足平行趋势假设，得到了更可靠的评估结果。

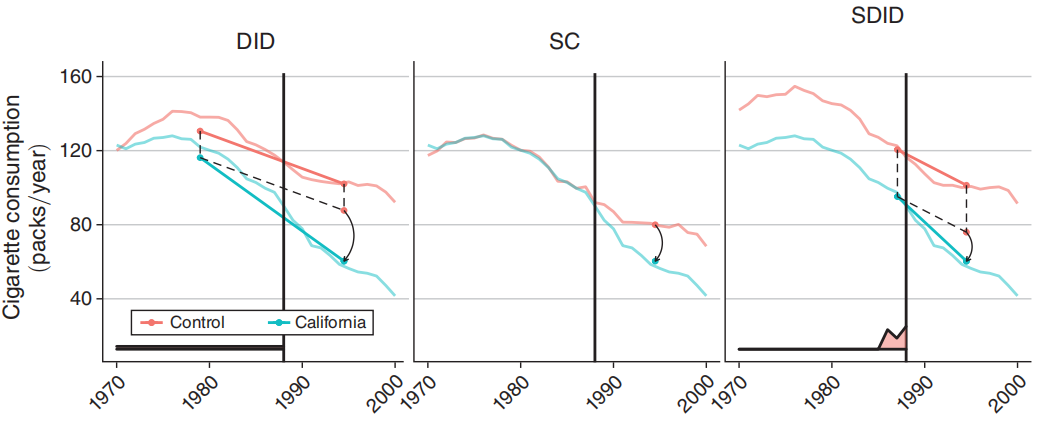
（2）估计量更稳健、精度更高。SDID通过双重权重优化，有效控制了个体异质性与时间异质性的干扰，其估计量在理论上具有一致性与渐近正态性。Arkhangelsky等（2021）在加州控烟法案例中对比了DID、SCM、SDID等五种方法，结果显示SDID的估计量标准误显著更小；同时SDID的处理效应估计值更接近真实政策效应，避免了DID因平行趋势不满足导致的高估问题。此外，SDID允许通过bootstrap、jackknife等方法进行稳健推断，解决了SCM难以可靠估计标准误的痛点。

（3）适用场景更广泛，兼容性更强。SDID打破了DID与SCM的适用场景限制：既适用于大量处理单元的大面板数据（如全国范围内的政策试点），也适用于单个/少量处理单元的案例研究（如某一重大工程的区域影响）；同时可无缝整合交错处理设计（即不同个体在不同时期接受处理的场景），通过sdid_event等Stata命令即可实现动态处理效应估计。这种广泛的适用性使其在经管科研的各类政策评估、效应识别场景中均能发挥作用。

（4）可灵活整合协变量，提升匹配质量。SDID允许在权重估计过程中引入协变量（如经济发展水平、产业结构、企业特征等），通过covariates选项实现“特征+趋势”的双重匹配。例如在评估企业政策效应时，可引入企业规模、资产负债率等协变量，使合成控制组与处理组在企业基本面特征上更相似，进一步提升反事实构建的准确性。

五、合成双重差分的主要局限

（1）对数据质量要求严苛。SDID要求面板数据必须高度平衡，即每个个体在每个时期都有完整的观测值，不能存在关键变量的缺失值。因为最优权重是基于处理前时期的全覆盖数据计算的，缺失值会导致权重估计失真。这在经管科研中可能构成较大限制，例如部分微观企业数据、县级层面的宏观数据常存在缺失值，需要进行复杂的数据清理与插补，增加了研究成本。

（2）权重估计存在敏感性与识别风险。SDID的核心是最优权重的估计，但权重结果可能受正则化参数选择、协变量设定的影响较大，不同的参数设定可能得到差异较大的权重，进而影响处理效应估计结果。此外，若控制组个体与处理组差异过大（即处理组不在控制组的凸包内），即使通过权重优化也难以构建有效的合成对照组，导致估计失效。这种权重敏感性要求研究者必须进行充分的稳健性检验（如权重扰动检验、控制组替换检验）。

（3）计算复杂度较高，对软件操作有一定要求。相较于传统DID的OLS估计，SDID的双重权重优化涉及复杂的最优化算法，虽然已有Damian Clarke等学者开发的sdid、sdid_event等Stata命令，但命令的参数设置（如vce类型选择、reps重复次数设定）需要研究者具备扎实的计量经济学基础。例如在选择方差估计方法时，bootstrap适用于大样本，jackknife适用于小样本，若选择不当会影响显著性推断结果。

（4）难以处理动态异质性处理效应。虽然SDID可通过sdid_event命令实现动态处理效应估计，但在存在强动态异质性（如处理效应随时间呈现非线性变化、不同队列处理单元的效应差异显著）的场景中，其估计效果仍有待提升。有研究表明，当政策效应存在滞后性或衰减性时，SDID对时间权重的依赖可能导致动态效应估计出现偏差。

六、总结与科研应用建议

合成双重差分（SDID）作为融合DID与SCM优势的前沿因果推断方法，通过双重权重优化实现了对平行趋势假设的放松与估计精度的提升，在经管科研的政策评估、企业行为、要素市场等多个领域具有广泛应用价值。但同时，SDID对数据质量的严苛要求、权重估计的敏感性也要求研究者在应用时保持谨慎。

基于前文分析，为各位科研工作者提出以下应用建议：一是明确方法适用条件，仅当处理组与控制组存在事前趋势差异、平行趋势假设难以满足时，优先选择SDID；二是严格把控数据质量，确保面板数据的平衡性与完整性，必要时进行数据插补与清理；三是重视稳健性检验，通过权重扰动、控制组替换、不同方差估计方法等多种方式验证结果的可靠性；四是结合研究场景灵活整合其他方法，如与机器学习结合提升权重估计精度，与空间计量结合控制空间溢出效应。

文献引用

Arkhangelsky D, Athey S, Hirshberg D A, et al. Synthetic difference-in-differences[J]. American Economic Review, 2021, 111(12): 4088-4118.