在机器学习领域，如果说有一个算法既“古老”又实用，那非朴素贝叶斯（Naive Bayes）莫属。这个看似“朴素”的算法，凭借其简单、高效、抗噪的特性，在文本分类、推荐系统等领域稳坐半壁江山。今天我们就来深入解析这个“朴素”却不简单的算法，看看它是如何在复杂场景中“以简胜繁”的。

一、从一个生活例子看懂朴素贝叶斯

 

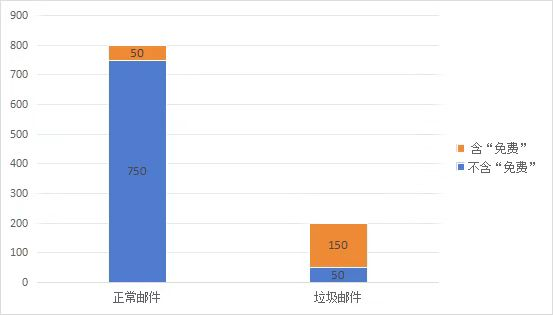
想象这样一个场景：你是公司的邮件管理员，每天处理1000封邮件，其中200封是垃圾邮件。在垃圾邮件中，有150封包含“免费”这个词；而在正常邮件中，只有50封包含“免费”。

现在收到一封新邮件，内容里有“免费”，它有多大可能是垃圾邮件？

这就是朴素贝叶斯要解决的典型问题：已知邮件含“免费”（特征），求它是垃圾邮件（类别）的概率。通过简单的概率计算，我们能得出这封邮件有75%的概率是垃圾邮件。

二、核心原理：贝叶斯定理 + “朴素”假设

（一）贝叶斯定理："由果推因"的概率公式

贝叶斯定理是18世纪英国数学家托马斯・贝叶斯提出的概率公式，其本质是通过已知的“结果”反推“原因”的概率。数学表达式为：

P(A|B) = P(B|A) × P(A) / P(B)

在邮件分类的语境中：

P(A|B)：后验概率，即已知邮件含“免费”(B)时，它是垃圾邮件(A)的概率

P(A)：先验概率，即邮件是垃圾邮件的概率（已知为20%）

P(B|A)：似然概率，即垃圾邮件中含“免费”的概率（75%）

P(B)：证据概率，即所有邮件中含“免费”的概率（20%）

代入计算：P(A|B) = (75% × 20%) / 20% = 75%

（二）“朴素”的关键：特征独立性假设

现实中的邮件特征远不止是否含“免费”，还可能包括是否含“中奖”、发送时间等。如果考虑n个特征，贝叶斯定理的计算会变得极其复杂。

朴素贝叶斯的“朴素”之处在于：假设所有特征之间相互独立。这意味着邮件含“免费”和“发送时间在深夜“这两个特征互不影响。

这一假设极大简化了计算：多个特征同时出现的概率等于每个特征单独出现的概率乘积。例如，同时含“免费”和“中奖”的垃圾邮件概率，可简化为P(免费|垃圾) × P(中奖|垃圾)。

（三）分类逻辑：概率最大原则

朴素贝叶斯的分类逻辑很直接：对一个样本，计算它属于每个类别的后验概率，选择概率最大的类别作为预测结果。

比如判断邮件类别时，分别计算它是“垃圾邮件”和“正常邮件”的后验概率，哪个概率大就归为哪类。

三、算法实现：从数学公式到步骤拆解

朴素贝叶斯的实现步骤可总结为“3算1比1预测”，以“判断邮件是否为垃圾邮件”为例：

（一）计算先验概率 P(类别)

即每个类别的出现概率：

垃圾邮件概率：P(垃圾) = 垃圾邮件数 / 总邮件数

正常邮件概率：P(正常) = 正常邮件数 / 总邮件数

（二）计算似然概率 P(特征|类别)

即每个特征在某个类别下的概率：

对离散特征（如含“免费”）：

P(含“免费”|垃圾) = 垃圾邮件中含“免费”的数量 / 垃圾邮件总数

对连续特征：

通常假设服从正态分布，计算概率密度函数值

（三）计算后验概率并预测

由于所有类别的P(特征)相同，只需比较P(类别) × P(特征|类别)，最终选择后验概率最大的类别。

四、优缺点及应用场景

（一）优点

1. 计算速度快

只涉及概率乘积和计数，无需复杂迭代

适合百万级数据的大规模处理

2. 小样本友好

即使训练数据有限，也能构建有效模型

3. 抗干扰能力强

对噪声数据和缺失值不敏感

特征冗余时仍能保持稳定表现

（二）缺点

1. 特征独立假设过于理想

现实中特征往往相关（如"免费"和"中奖"常同时出现）

强相关特征会降低模型精度

2. 无法学习特征依赖关系

不能捕捉特征间的联动效应

比如“雨天+周末”对出行的影响无法准确建模

3. 对分布假设敏感

连续特征若不服从假设的分布（如正态分布），结果会出现偏差

（三）应用场景

1. 文本分类

垃圾邮件过滤、新闻分类、情感分析

特别适合处理词袋模型，特征独立性假设近似成立

2. 推荐系统

结合用户历史行为，预测“用户喜欢某商品”的概率

在协同过滤中作为基础分类器

3. 医疗诊断

根据“咳嗽+发烧”等症状组合，预测患某种疾病的概率

辅助医生进行初步诊断

4. 欺诈检测

通过“异地登录+大额转账”等特征组合，识别信用卡盗刷行为

在金融风控中发挥重要作用

 

参考文献

[1] Duda R O, Hart P E. Pattern classification and scene analysis[J]. A Wiley-interscience publication, 1973.

[2] Ke Z T, Kelly B T, Xiu D. Predicting returns with text data[R]. National Bureau of Economic Research, 2019.

[3] Laplace P S. Mémoire sur la probabilité de causes par les évenements[J]. Mémoire de l'académie royale des sciences, 1774.

[4] Li Y, Osei F B, Hu T, et al. Urban flood susceptibility mapping based on social media data in Chengdu city, China[J]. Sustainable Cities and Society, 2023, 88: 104307.

[5] Xie C, Yang X, Chen T, et al. Short-term wind power prediction framework using numerical weather predictions and residual convolutional long short-term memory attention network[J]. Engineering Applications of Artificial Intelligence, 2024, 133: 108543.

[6] Zhang H. The optimality of naive Bayes[J]. Aa, 2004, 1(2): 3.