在机器学习工作流中,寻找模型最佳超参数无疑是最具挑战性的环节之一。模型的性能与超参数的选择直接相关,良好的调参能让模型表现大幅提升,而糟糕的参数选择则可能让优秀算法黯然失色。
深入解析机器学习中四种常用的调参方法,从基础到高级,找到模型优化的“金钥匙”。
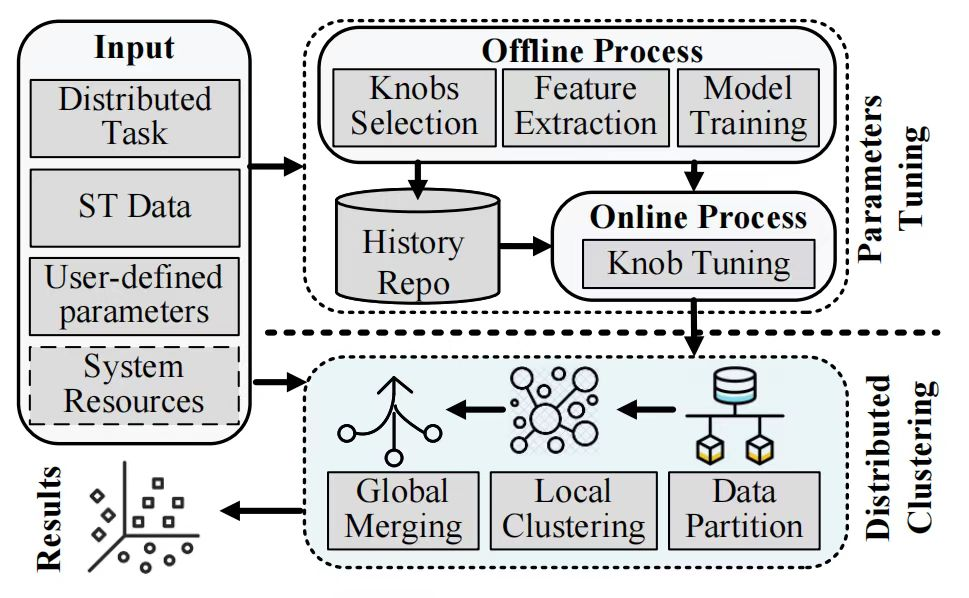
图片来源:Li et al.(2025)
一、传统手工调参:最原始的调优艺术
手工调参是最基础、最直观的方法。研究人员通过训练算法手动检查随机超参数组合,然后选择符合目标的最佳参数集。
代码示例:
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, KFold, cross_val_score
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target
# 分割数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=14)
# 定义参数网格
k_value = list(range(2,11))
algorithm = ['auto','ball_tree','kd_tree','brute']
scores = []
best_comb = []
kfold = KFold(n_splits=5)
# 手工调参循环
for algo in algorithm:
for k in k_value:
knn = KNeighborsClassifier(n_neighbors=k,algorithm=algo)
results = cross_val_score(knn,X_train,y_train,cv=kfold)
print(f'Score:{round(results.mean(),4)} with algo = {algo} , K = {k}')
scores.append(results.mean())
best_comb.append((k,algo))
best_param = best_comb[scores.index(max(scores))]
print(f'\nThe Best Score : {max(scores)}')
print(f"['algorithm': {best_param[1]} ,'n_neighbors': {best_param[0]}]")
缺点分析:
无法保证获得全局最优参数组合
完全依赖研究人员的经验和直觉
极其耗时,效率低下
二、网格搜索:系统化的参数扫描
网格搜索是一种系统化的超参数调优技术。它为指定网格中所有超参数值的每个排列构建模型,通过评估选择最佳模型。
工作原理:
假设有两个超参数 k_value = [2,3,4,5,6,7,8,9,10] 和 algorithm = ['auto','ball_tree','kd_tree','brute'],网格搜索将构建9×4=36个不同的模型进行全面比较。
sklearn实现:
from sklearn.model_selection import GridSearchCV
knn = KNeighborsClassifier()
grid_param = { 'n_neighbors' : list(range(2,11)) ,
'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
grid = GridSearchCV(knn,grid_param,cv=5)
grid.fit(X_train,y_train)
# 最佳参数组合
print(grid.best_params_)
# 最佳得分
print(grid.best_score_)
核心优势:
系统性:确保不会遗漏任何参数组合
确定性:给定相同的参数空间,结果可重现
明显短板:
计算成本高,速度慢
参数维度灾难:超参数数量增加会指数级增加计算时间
资源消耗大
三、随机搜索:效率与效果的平衡艺术
随机搜索从超参数空间中随机选择参数组合,在固定的迭代次数内寻找最优解。研究表明,在许多情况下,随机搜索的结果优于网格搜索。
为什么随机搜索更有效?
并非所有超参数对模型性能的影响程度相同。随机搜索通过随机采样,更有可能在有限迭代内找到重要参数的最佳范围。
实现方式:
from sklearn.model_selection import RandomizedSearchCV
knn = KNeighborsClassifier()
grid_param = { 'n_neighbors' : list(range(2,11)) ,
'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
rand_ser = RandomizedSearchCV(knn,grid_param,n_iter=10)
rand_ser.fit(X_train,y_train)
# 最佳参数组合
print(rand_ser.best_params_)
# 最佳得分
print(rand_ser.best_score_)
优势分析:
计算效率高,特别适合高维参数空间
在实际应用中往往能找到与网格搜索相当甚至更好的结果
资源消耗可控
局限性:
不能保证找到全局最优解
结果具有一定随机性
四、贝叶斯搜索:智能化的参数优化
贝叶斯优化属于基于序列模型的优化(SMBO)算法类别。它使用先前对目标函数的观察结果,智能地确定下一个最优点进行采样。
算法核心思想:
构建目标函数的概率模型(通常使用高斯过程)
利用该模型选择最有希望的超参数组合
根据真实评估结果更新模型
重复过程直到满足停止条件
scikit-optimize实现:
from skopt import BayesSearchCV
import warnings
warnings.filterwarnings("ignore")
from skopt.space import Real, Categorical, Integer
knn = KNeighborsClassifier()
# 定义超参数网格
grid_param = { 'n_neighbors' : list(range(2,11)) ,
'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
# 初始化贝叶斯搜索
Bayes = BayesSearchCV(knn, grid_param, n_iter=30, random_state=14)
Bayes.fit(X_train,y_train)
# 最佳参数组合
print(Bayes.best_params_)
# 最佳得分
print(Bayes.best_score_)
贝叶斯优化的独特优势:
自适应采样:根据历史结果智能选择下一个采样点
样本效率高:通常能用更少的迭代找到优质解
特别适合评估成本高的场景
需要注意的缺点:
算法本身复杂度较高
低维空间中优势明显,但随着维度增加需要更多样本
参考文献
[1] Li, J., Gou, S., Li, R., He, H., Li, W., & Zheng, Y. (2025). DiST: Efficient Distributed Spatio-Temporal Clustering With Automatic Parameter Optimization. IEEE Transactions on Knowledge and Data Engineering.
[2] Lund, J. W., Groten, J. T., Karwan, D. L., & Babcock, C. (2022). Using machine learning to improve predictions and provide insight into fluvial sediment transport. Hydrological Processes, 36(8), e14648.
[3] Chen, Y., Chen, Z., Xu, D., Li, S., Chen, F., Yu, X., ... & **ao, S. (2025). Early prediction of bloodstream infections in ICU patients using machine learning methods based on routine laboratory parameters. BMC Infectious Diseases, 25(1), 1196.
[4] Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., ... & Duchesnay, É. (2011). Scikit-learn: Machine learning in Python. the Journal of machine Learning research, 12, 2825-2830.

